W poprzednich rozważaniach zakładaliśmy, że dodawane wektory są podobnego typu; tzn. wektory przemieszczenia są dodawane do wektorów przemieszczenia, wektory prędkości do wektorów prędkości itd. Tak samo jak nie ma sensu dodawanie wielkości skalarnych różnego rodzaju, takich jak masa i temperatura, nie ma też sensu dodanie wielkości wektorowych różnego rodzaju, np. przemieszczenia i natężenia pola elektrycznego.
       Jednakże, podobnie jak w przypadku skalarów, różne rodzaje wektorów możemy mnożyć przez siebie tworząc nowe wielkości fizyczne, o nowych wymiarach. Ponieważ wektory mają określoną zarówno wartość bezwzględną, jak i kierunek, mnożenie wektorowe nie może podlegać dokładnie tym samym regułom algebraicznym co mnożenie skalarne. Musimy ustalić nowe reguły mnożenia wektorów.
       Omówimy jedynie definicje trzech najczęściej stosowanych rodzajów mnożenia wektorów:

1. mnożenie wektora przez skalar,
2. mnożenie dwóch wektorów, w taki sposób, aby iloczyn ich był skalarem,
3. mnożenie dwóch wektorów w taki sposób, aby dawały one nowy wektor.

Istnieją jeszcze inne możliwości, ale nie będziemy ich tutaj rozpatrywać.
       Mnożenie wektora przez skalar ma prostą interpretację: iloczyn skalara k i a, zapisywany jako ka, jest z definicji nowym wektorem, o wartości k razy większej od wartości wektora a. Nowy wektor ma taki sam zwrot jak a, jeżeli k jest dodatnie, a zwrot przeciwny, w przypadku gdy k jest ujemne. Aby podzielić wektor przez skalar, po prostu mnożymy wektor przez odwrotność skalara.
       Sprawdź to mnożenie skalarne na amimacji "Iloczyn skalarny".
       Kiedy mnożymy wielkość wektorową przez inną wielkość wektorową, musimy rozróżniać między iloczynem skalarnym (oznaczonym kropką) i iloczynem wektorowym (oznaczonym krzyżykiem). Iloczyn skalarny dwóch wektorów a i b, oznaczany symbolem 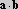, jest zdefiniowany następująco:

,
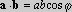gdzie a jest wartością bezwzględną wektora a, b - wartością bezwzględną b, a 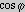- cosinusem kąta zawartego między tymi dwoma wektorami (patrz rysunek 11).
       Ponieważ a i b są skalarami, a 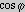- zwykłą liczbą, a więc iloczyn skalarny dwóch wektorów jest skalarem. Iloczyn ten można traktować jako iloczyn wartości bezwzględnej jednego wektora i składowej drugiego wektora wzdłuż kierunku pierwszego.
       Iloczyn a i b moglibyśmy zdefiniować w jakikolwiek inny sposób, przyjmując np., że jest on równy a^1/3b^1/3tg/2, ale taka definicja nie miałaby żadnego zastosowania w fizyce. Przy naszej definicji iloczynu skalarnego wiele ważnych wielkości fizycznych da się przedstawić w postaci iloczynu skalarnego dwóch wektorów. Jako przykłady można podać: pracę mechaniczną, grawitacyjną, energię potencjalną, potencjał elektryczny, moc elektryczną oraz gęstość energii elektromagnetycznej.
       Iloczyn wektorowy dwóch wektorów, oznaczany symbolem 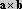, jest nowym wektorem c, przy czym c=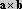. Wartość bezwzględna wektora c jest określona równaniem:

,
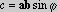gdzie jest kątem zawartym między wektorami a i b.
       Kierunek wektora c będącego iloczynem wektorowym dwóch wektorów a i b jest z definicji prostopadły do płaszczyzny utworzonej przez te dwa wektory. Aby określić dodatni zwrot wektora c, musimy odwołać się do rysunku 12. Wyobraźmy sobie, że śruba prawoskrętna, której oś jest prostopadła do płaszczyzny utworzonej przez wektory a i b, obraca się od wektora a do wektora b o kąt równy kątowi zawartemu między tymi wektorami. 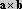Kierunek poruszania się śruby określa dodatni kierunek iloczynu wektorowego (rysunek 12a). Inny wygodny sposób określania kierunku iloczynu wektorowego jest następujący. Wyobraźmy sobie oś prostopadłą do płaszczyzny utworzonej przez wektory a i b, i przechodzšcą przez ich wspólny początek. Następnie owińmy palce prawej ręki wokół tej osi i pchnijmy czubkami palców wektor a w stronę wektora b, poprzez mniejszy kąt między tymi wektorami, trzymając kciuk wyprostowany; kierunek kciuka wskaże wówczas kierunek iloczynu wektorowego 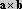(rysunek 12b).
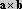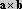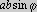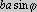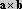       Zauważmy, że iloczyn nie jest tym samym wektorem co iloczyn ; oznacza to, że w iloczynie wektorowym ważny jest porządek czynników. Zupełnie inaczej jest w wypadku skalarów, ponieważ w algebrze i arytmetyce kolejność czynników nie wpływa na ostateczny wynik. W przypadku iloczynu wektorowego = - (rysunek 12c). Można to wywnioskować z faktu, że wartość równa jest wartości , natomiast zwrot jest przeciwny do zwrotu ; wynika to stąd, że śruba prawoskrętna porusza się w jednym kierunku, gdy obracamy ją od a do b poprzez kąt , i w kierunku przeciwnym, gdy obraca się ona od b do a poprzez ten sam kąt . Taki sam wynik otrzymalibyśmy stosując regułę prawej ręki.
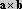       Jeżeli = 90°, wektory a, b i c (c = ) tworzą nawzajem ze sobą kąty proste i wskazują kierunek osi trójwymiarowej, prawoskrętnego układu współrzędnych.
       Podana wyżej definicja iloczynu wektorowego została wybrana dlatego, że okazała się bardzo użyteczna w fizyce. Często spotykamy wielkości fizyczne będące wektorami, których iloczyn wektorowy zdefiniowany w powyższy sposób jest wielkością wektorową mającą ważne znaczenie fizyczne. Przykładami wielkości fizycznych będących iloczynami wektorowymi są moment siły, moment pędu, siła działająca na ładunek poruszający się w polu magnetycznym oraz strumień energii elektromagnetycznej.
       Iloczyn skalarny jest najprostszym iloczynem dwóch wektorów. Iloczyn wektorowy jest następnym z kolei prostym przypadkiem. Tutaj kolejność mnożenia wpływa jedynie na znak iloczynu, co oznacza odwrócenie zwrotu. Znane są również inne iloczyny wektorów, równie pożyteczne, ale bardziej skomplikowane. Można na przykład utworzyć tensor, mnożąc kolejno każdą z trzech składowych jednego wektora przez trzy składowe drugiego wektora. Taki tensor (drugiego rzędu) utworzony jest więc z dziewięciu liczb, wektor z trzech liczb, a skalar tylko z jednej liczby. Przykładami wielkości fizycznych, które można przedstawić za pomocą tensora, są naprężenie mechaniczne i elektryczne, momenty bezwładności i odkształcenia.
       Sprawdź to mnożenie wektorowe na amimacji "Iloczyn wektorowy".